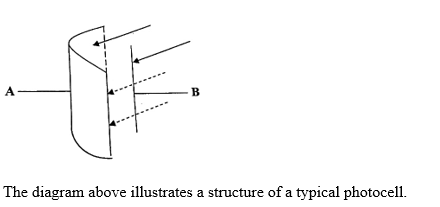
The diagram above illustrates a structure of a typical photocell. (i) Identify each of the parts labelled A and B. (ii) State one function each of A and B (...

Answer Details

(a)

(i) A - Metal surface, B - Collector electrode

(ii) A - To emit electrons when photons hit its surface, B - To collect the emitted electrons and create a current.

(iii) E represents the energy of the photon, hf represents the energy of the photon before it hits the metal surface, and Wo represents the work function or the minimum energy required to remove an electron from the metal surface.

(b)

Using Einstein's photoelectric equation, we can write:
hf = E + Wo
where hf is the energy of the photon, E is the kinetic energy of the emitted electron, and Wo is the work function.

We know that E = 1.97 eV and Wo = 1.32 eV. Converting to joules, we have:
E = 1.97 x 1.6 x 10^-19 J = 3.15 x 10^-19 J
Wo = 1.32 x 1.6 x 10^-19 J = 2.11 x 10^-19 J

Substituting these values into the equation:
hf = E + Wo = 3.15 x 10^-19 J + 2.11 x 10^-19 J = 5.26 x 10^-19 J

Finally, using the formula for the energy of a photon:
E = hf = hc/λ
where h is Planck's constant, c is the speed of light, and λ is the wavelength of the photon. Solving for λ, we get:

λ = hc/E = (6.626 x 10^-34 J s x 3.0 x 10^8 m/s) / 5.26 x 10^-19 J = 3.77 x 10^-7 m

So, the frequency of the photon is:
f = c/λ = 3.0 x 10^8 m/s / 3.77 x 10^-7 m = 7.96 x 10^14 Hz

(c)

(i) The half-life of a radioactive element is the time taken for half of the radioactive nuclei to decay.

(ii) The graph of the relation N = Noe^-λt is an exponential decay curve. The half-life can be found by setting N = 0.5No and solving for t. This gives:

0.5No = Noe^-λt

Taking the natural logarithm of both sides, we get:

ln(0.5) = -λt1/2

where t1/2 is the half-life. Rearranging this equation, we get:

t1/2 = ln(2) / λ

The half-life is the time taken for the number of radioactive nuclei to reduce to half its initial value, as shown in the graph.